Newton's approximation of Pi

Over the centuries, many amateur and professional mathematics have taken up the challenge of calculating p to more and more decimal places. Much effort has gone into performing the exhausting calculations required and looking for series that reach the desired answer faster. For some, it becomes an obsession. Isaac Newton (1642-1727) admitted as much in 1666 when he wrote, "I am ashamed to tell you to how many figures I carried these computations, having no other business at the time." He managed to compute at least 15 digits using the formula Pi :

The following is an explanation of Newton’s approximation of Pi:

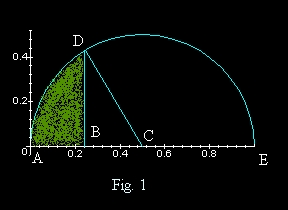
Newton had certainly mastered the concepts of analytic geometry, and he cast his work in this format. He began with a semicircle having its center C at (1/2, 0) and radius r=1/2, as shown in Fig.1.

He knew that the circle’s equation was

Simplify and solving for y gives the equation of the upper semicircle as

then from there the expression can be replaced by its binomial expansion, thus giving the equation of the semi-circle as:

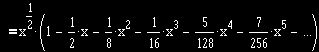
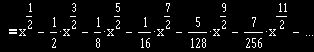
From there Isaac Newton, using his genius brain, let B be the point (1/4,0), as indicated in Fig.!. Then he drew BD perpendicular to the semicircle’s diameter AE. He then worked with the shaded are ABD in two very different ways:

1.Area (ABD) by fluxions:

In order to continue on explaining how Isaac Newton worked with that area, it is essential to explain briefly the rules of De Analysi.

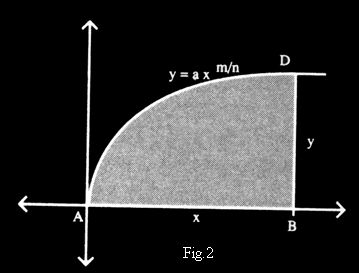
In Figure 2, Newton was finding the are above the horizontal axis, beneath the curve , and so far to the right as the point x. According to Newton, this area was

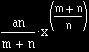Further, as Newton explained in Rule 2 of De Analysi, "If the value of y be made up of several terms, the Area likewise shall be made up of the Areas which result from everyone of the terms." As an example, he noted that the area beneath the curve is just:

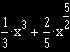
Now returning to the explanation. Using the rules of the De Analysi, the shaded area can be simply written as:

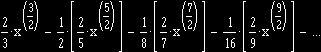This simplification would therefore be evaluated for x=1/4. The genius of his approach is that the resulting simplifies beautifully when we evaluate it, since

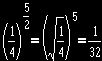
and so on. Thus we approximate the shaded area (ABD), using the first nine terms of the simplified series and we end up with an approximation of 0.07677310678.

2. Area (ABD) by geometry:

Newton next reexamined the problem of the shaded area using simple geometry. He first determined the area of the right triangle DDBC. Also, notice that the length of BC is ¼, while CD, being a radius, has length r=1/2. Simply applying the Pythagorean theorem yielded :

Therefore,

Next, Newton wanted the area of the pie shaped sector ACD. To determine this area, he simply referred to DDBC. With the length of BC being exactly half that of the hypotenuse CD, he recognized this as a familiar 30°-60°-90° right triangle. ÐBCD was a 60° angle. Knowing that the angle of the sector was 60°- that is, one-third of the 180° angle forming the semicircle- Newton could see that the area of the sector was likewise a third of the area of the semicircle. In other words:

At last P has appeared in Newton’s huge chain of reasoning. All there is left is a final step to two to get a wonderfully efficient approximation of it. Thus the geometric approach to the shaded area gives us:

All we have got to do is simply equating this result with the fluxion-binomial theorem approximation for the same shaded area from above. We therefore have, and solving for Pi gives us the estimate