PROOF
Euler began his proof by introducing the function
![]()
To Euler, f (x) was just an infinite polynomial with f (0) = 1. Thus, it can be factored provided the roots of the equation f (x) = 0 are determined. Keeping in mind that x is not equal to zero:
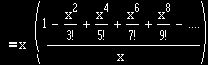

![]() , by the
Taylor Expansion of sin x
, by the
Taylor Expansion of sin x
Then, as long as x is not 0, solving f (x) amounts to solving 0![]() ,
which by using a simple cross-multiplication, reduces to solving sin (x)
= 0. The sine function equals 0 precisely for x = 0, x = + /- Pi, x = +/-
2Pi..... But we have to eliminate x = 0 from consideration as a solution
to f (x) = 0, since we have already noted that f (0) = 1. Using these considerations,
Euler factored f (x) as:
,
which by using a simple cross-multiplication, reduces to solving sin (x)
= 0. The sine function equals 0 precisely for x = 0, x = + /- Pi, x = +/-
2Pi..... But we have to eliminate x = 0 from consideration as a solution
to f (x) = 0, since we have already noted that f (0) = 1. Using these considerations,
Euler factored f (x) as:
![]() ....
....
![]()
which amounts to
![]()
= ![]()
This is a pretty cool result because it changes an infinite sum
with an infinite product. Which means that the infinite series by which
f (x) was originally defined has been equated to the infinite product on
the right. Euler then went on by multiplying out the infinite product
on the right side of the preceding equation and then collecting all terms
having the same power of x. In doing so, the first term to appear would
be the product of all of the 1s (which turns out to be 1). To end up with
an ![]() term, we would
have to multiply the 1s from all but one of the factors by an
term, we would
have to multiply the 1s from all but one of the factors by an ![]() tern
from that remaining factor. Then Euler's infinite multiplication problem
would give us this equation:
tern
from that remaining factor. Then Euler's infinite multiplication problem
would give us this equation:
![]()
=![]()
=![]()
After Euler had multiplied out the infinite product to get two infinite
sums equal to each other, he went on to equate the like powers of x. Next
comes the ![]() term
in each series, and so the coefficients must be equal, which is:
term
in each series, and so the coefficients must be equal, which is:
![]()
Then multiplying both sides by -1, and making 3! = 6 on the left side,
and factoring the common ![]() ,
Euler arrived at
,
Euler arrived at
![]()
and then a final cross multiplication yielded the astonishing fact that
![]()
Q.E.D.
|Main||History of Pi||Formulas||Programs||Authors||References|